$z^a$ Circle Pattern
Jürgen Richter-Gebert, Jan TechterMedia
Description
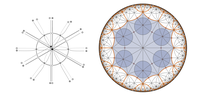
The Cinderella Applet [$z^a$ Cinderella Exhibit] shows the circle pattern that corresponds to a discrete version of the complex map $z \mapsto z^a$ for $0 \lt a \lt 2$.
The centers of the circles and their intersection points are given by the discrete map $f:\mathbb{Z}^2_+ \rightarrow \mathbb{C}$ on the first quadrant $\mathbb{Z}^2_+$ of the lattice $\mathbb{Z}^2$ that is characterized by the initial values $$ f_{0,0} = 0, \quad f_{1,0} = 1, \quad f_{0,1} = e^{i\frac{\pi}{2}a} \tag{IV} $$ and the two conditions $$ \frac{ (f_{m,n} - f_{m+1,n}) }{ (f_{m+1,n} - f_{m+1,n+1}) } \frac{ (f_{m+1,n+1} - f_{m,n+1}) }{ (f_{m,n+1} - f_{m,n}) } = -1 \tag{1} $$ $$ a f_{m,n} = 2m \frac{ (f_{m+1,n} - f_{m,n})(f_{m,n} - f_{m-1,n}) }{ f_{m+1,n} - f_{m-1,n} } + 2n \frac{ (f_{m,n+1} - f_{m,n})(f_{m,n} - f_{m,n-1}) }{ f_{m,n+1} - f_{m,n-1} } \tag{2} $$ Condition (1) means that all elementary quadrilateral are conformal squares, i.e. the cross ratio of its vertices are equal to $-1$. This condition is Möbius invariant and allows to compute all values of $f$ from the values $f_{m,0}$ and $f_{0,n}$ on the axes.
Condition (2) is compatible with condition (1) and describes some isomonodromic solutions of the latter. It can be used to compute the values $f_{m,0}$ and $f_{0,n}$ from the initial values (IV). Its smooth limit corresponds to the smooth $z^a$.
Move the y-axis to adjust (IV) in terms of the angle $\varphi = \frac{\pi}{2}a$ between the axes. For $\varphi \in (0,\pi)$ the power $a$ runs between $0$ and $2$ and the so obtained discrete map has no overlapping neighboring quadrilaterals, i.e. is an immersion, which was shown in [1]. Besides, one can adjust $\varphi$ to obtain any $a \in (-\infty,\infty)$, but the corresponding circle patterns are no longer immersed.
The discrete $z^a$ map for $0 \lt a \lt 2$ was introduced in [2]. A detailed description can also be found in [1] and [3]. The asymptotic behaviour at infinity was proven in [4]. The first implementations of the $z^a$ circle pattern were done by Tim Hoffmann, see also [5].
References
-
Alexander I. Bobenko and Sergey I. Agafonov.
Discrete Zγ and Painlevé equations.
International Mathematics Research Notices, 2000(4):165–193, January 2000.
URL: http://oup.prod.sis.lan/imrn/article-pdf/2000/4/165/1951661/2000-4-165.pdf, doi:10.1155/S1073792800000118. -
Alexander I. Bobenko.
Symmetries and Integrability of Difference Equations.
London Mathematical Society Lecture Notes, 1999.
-
Alexander I. Bobenko and Yuri B. Suris.
Discrete Differential Geometry: Integrable Structure.
American Mathematical Society, 2009.
-
A. I. Bobenko and A. Its.
The asymptotic behaviour of the discrete holomorphic map $Z^a$ via the Riemann-Hilbert method.
Duke Math. J., 2015. accepted.
arXiv:1409.2667. -
Tim Hoffmann.
Conformally Symmetric Circle Packings.
2001.
URL: http://page.math.tu-berlin.de/~hoffmann/interactive/cscpOnline/Applets.html.