CMC Noids - Constant Mean Curvature Surfaces in Euclidean 3-Space

Description

---

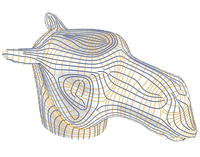
There a loads of examples of so called "Noids", that is constant mean curvature surfaces in euclidean 3-space shown here.

Further, there are Noids with platonic symmetries, "Platonic Noids".

The "Symmetric Fournoids" are four-punctured spheres with asymptotically Delaunay ends. These fournoids are constructed by lifting a trinoid-like surface on a three-punctured sphere to a multiply-punctured sphere.

The naked trinoid dressed by simple factors acquires bubbles which can squiggle at the trinoid's center or glissade off its ends. In the images, the maximal constant mean curvature trinoid is fleshed out with a four-lobed bubbleton. Three of its lobes have separated and are undulating along the upward end, to eventually disappear leaving a single lobe at the center. The images show the whole surface together with two non-symmetric halves. These surfaces were discovered by Nick Schmitt and Philipp Lang based on the theory of dressed n-noids.

N-noids are constant mean curvature (CMC) immersions of a n-punctured Riemann sphere into Euclidean 3-space with ends asymptotic to CMC Delaunay half-cylinders of revolution.
These fournoids were constructed by the loop group Weierstrass representation of CMC surfaces. Unlike n-noids with Platonic symmetries, which are based on trinoids and hence have no accessory parameters in their Weierstrass representations, these surfaces have infinitely many accessory parameters, which were computed by numerical search.
The lines on the red surfaces are curvature lines meeting at four umblics, two of which are visible in each image. The end axes, while colplanar, are not concurrent.

In contrast to k-noids, with Fuchsian DPW potentials, these CMC cylinders and trinoids come from potentials with one or more irregular singular points. Instead of being asymptotic to Delauany cylinders, the ends of these surfaces behave similarly to those of Smyth surfaces.

References

---

Authors

See also