Dual del Pezzo 4-Polytope
Benjamin Assarf, Michael JoswigMedia
Description
The del Pezzo polytope of dimension $d$ is the convex hull of the $2d+2$ points $\{\pm e_1,\pm e_2, \dots, \pm e_d, \pm \mathbf{1}\}$. The Del-Pezzo polytopes are lattice polytopes which are terminal and reflexive. If $d$ is even the del Pezzo $d$-polytope is a smooth Fano polytope.
A $\textit{lattice polytope}$ $P$ is a convex polytope whose vertices lie in the lattice $\mathbb{Z}^d$ contained in the vector space $\mathbb{R}^d$. Fixing a basis of $\mathbb{Z}^d$ describes an isomorphism to $\mathbb{Z}^d$. A $d$-dimensional lattice polytope $P\subset\mathbb{R}^d$ is called $\textit{reflexive}$ if it contains the origin $0$ as an interior point and its polar polytope is a lattice polytope. A lattice polytope $P$ is $\textit{terminal}$ if $0$ and the vertices are the only lattice points in $P\cap \mathbb{Z}^d$. It is $\textit{simplicial}$ if each face is a simplex. We say that $P$ is a $\textit{smooth Fano polytope}$ if $P\subseteq \mathbb{R}^d$ is simplicial with $0$ in the interior and the vertices of each facet form a lattice basis of $\mathbb{Z}^d$. The fan where every cone is the non negative linear span over a face is called the $\textit{face fan}$. It is dual to the $\textit{normal fan}$, which is the collection of all normal cones.
The interest in classifications of smooth Fano polytopes has its origins in applications of algebraic geometry to mathematical physics. For instance, Batyrev [1] uses reflexive polytopes to construct pairs of mirror symmetric Calabi-Yau manifolds; see also [2].
In algebraic geometry, reflexive polytopes correspond to $\textit{Gorenstein toric Fano varieties}$. The toric variety $X_P$ of a polytope $P$ is determined by the face fan of $P$, that is, the fan spanned by all faces of $P$; see Ewald [3] or Cox, Little, and Schenck [4]. The toric variety $X_P$ is $\mathbb{Q}$-$\textit{factorial}$ (some multiple of a Weil divisor is Cartier) if and only if the polytope $P$ is simplicial. In this case the $\textit{Picard number}$ of $X$ equals $n-d$, where $n$ is the number of vertices of $P$. The polytope $P$ is smooth if and only if the variety $X_P$ is a manifold (that is, it has no singularities).
In 2006 Casagrande [5] proved that the number of vertices of $d$-di\-men\-sional simplicial, terminal, and reflexive lattice polytopes does not exceed $3d$. Those polytopes are classified if the number of vertices is greater or equal $3d-2$ (see [5] [6] [7]).
If you have two smooth Fano polytopes $P$ and $Q$, then the free sum $P\oplus Q$ is also smooth Fano. The same holds for a bipyramid over a smooth Fano polytope. A natural question to ask is how many smooth Fano polytopes are a free sum or a bipyramid over lower dimensional ones.
$\textbf{Conjecture:}$ Let $P$ be a $d$-dimensional smooth Fano polytope with $n$ vertices such that $n\ge 3d-k$ for $k\le\tfrac{d}{3}$. If $d{+}k$ is even then $P$ is lattice equivalent to $Q\oplus P_6^{\oplus (\frac{d-3k}{2})}$ where $Q$ is a $3k$-dimensional smooth Fano polytope with $n-3d+9k\ge 8k$ vertices. If $d{+}k$ is odd then $P$ is lattice equivalent to $Q\oplus P_6^{\oplus (\frac{d-3k-1}{2})}$ where $Q$ is a $(3k{+}1)$-dimensional smooth Fano polytope with $n-3d+9k-3\ge 8k-3$ vertices.
A recent result [8] supports this conjecture.
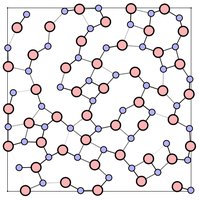
One example of a polytope which is not a free sum or a bipyramid over some lower-dimensional smooth Fano polytope is the del Pezzo $4$-polytope, which has $10 = 3\cdot 4-2$ vertices and $30$ facets. A Schlegel diagram of the dual del Pezzo $4$-polytope is visualized in [Fig 1]. One can download the $4$-dimensional del Pezzo polytope as a $\texttt{polymake}$ file in [data]. For $\texttt{polymake}$ check: www.polymake.org
References
-
Victor V. Batyrev.
Dual polyhedra and mirror symmetry for Calabi–Yau hypersurfaces in toric varieties.
J. Alg. Geom, pages 493–535, 1994.
-
Victor V Batyrev and Lev A Borisov.
Mirror duality and string-theoretic Hodge numbers.
Inventiones mathematicae, 126(1):183–203, 1996.
-
Günter Ewald.
Combinatorial convexity and algebraic geometry.
Springer, 1996.
-
David A. Cox, John B. Little, and Henry K. Schenck.
Toric varieties.
American Mathematical Society, 2011.
-
Cinzia Casagrande.
The number of vertices of a Fano polytope.
Annales de l'Institut Fourier, 56(1):121–130, 2006.
URL: https://aif.centre-mersenne.org/item/AIF_2006__56_1_121_0, doi:10.5802/aif.2175. -
Mikkel Øbro.
Classification of terminal simplicial reflexive d-polytopes with 3d − 1 vertices.
manuscripta mathematica, 125(1):69–79, January 2008.
doi:10.1007/s00229-007-0133-z. -
Benjamin Assarf, Michael Joswig, and Andreas Paffenholz.
Smooth Fano Polytopes with Many Vertices.
Discrete Computational Geometry, Springer US, 2014(52):153–194, 2014.
doi:10.1007/s00454-014-9607-4. -
Benjamin Assarf and Benjamin Nill.
A bound for the splitting of smooth Fano polytopes with many vertices.
Journal of Algebraic Combinatorics, 43(1):153–172, 2016.
doi:10.1007/s10801-015-0630-1.