Space Curves
Nicholas SchmittDescription
Elastic plane curves are finite type curves in 2-dimensional spaceforms. These curve minimize the total squared curvature. These curves were investigated by Euler in 1744 [1].
Figure 1depicts the elastic plane curves in $\mathbb{R}^2$ of spectral genus 1 are shown in the first figure. The 1-looped example (fourth from left) with singular spectral curve demarcates the orbitlike (left) from the wavelike (right). The orbitlike starting at the singular example flow left, converging to a circle. The wavelike starting at the singular example flow right, passing through the closed Euler lemniscate, converging to a straight line.
Figure 2 depicts a sampling of closed finte type curves in $S^2$ with low spectral genus. The elastic curve (first curve) with spectral genus 1 and six lobes, is symmetric about the equator. It can flow isoperiodically through constrained elastic curves with spectral genus 2 (second curve). The lemniscate (third curve) has spectral genus 1. These curves are profile curves of constrained Willmore Hopf tori[2][3].
Figure 3 depicts a sampling of elastic curves in $H^2$ of spectral genus 1. The first three curve are wavelike. The last two closed orbitlike curves are related to profile curves of constant mean curvature tori of revolution[3][4].
Circletons are finite type curves in Euclidean space. Figure 4 depicts closed planar simple circletons (simple factor dressings of the circle) in $\mathbb{R}^2$. These curves are parametrized by pairs of positive integers $(\ell, w)$ satisfying $\ell < w$, where $\ell$ is the lobe count and $w$ is the wrapping number of the underlying circle. The image depicts circletons for small $\ell$ and $w$: the rows are indexed by $w=2,…,7$ and the columns by $\ell=1,…,w-1$.
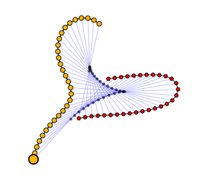
Figure 5 depicts the border line elastic curve, the unique (up to homothety) elastic planecurve in $\mathbb{R}^2$ with singular spectral curve. With arclength parametrization $(t-tanh 2t,sech 2t)$, it is a simple factor dressing of the vacuum $(t,\,0)$. As indicated by the struts, the pointwise distance between the straight line and the Euler loop as arclength parametrized curves is constant 1.
Figure 6 depicts an isospectral flow through closed simple circletons (simple factor dressings of the circle) in $\mathbb{R}^3$. From right to left, the planar circleton (also appearing in the top row of the first figure) deforms to a 2-wrapped circle in the limit. The spectral curve for this family is singular with algebraic genus 2 and geometric genus 0.
Figure 7 depicts The Euler lemniscate (first curve), the unique closed elastic planecurve in $\mathbb{R}^2$ up to homothety; it is finite type with spectral genus 1. The image shows two views of the spacecurve in $\mathbb{R}^3$ constructed by dressing the Euler lemniscate by a simple factor, preserving closing Its spectral curve is singular.
At last we see flows through finite type spacecurves in Euclidean 3-space. Figure 8 depicts an isospectral flow through closed finite type spacecurves in $\mathbb{R}^3$ of spectral genus 2. The curve returns to a translation of itself. This is an example of a vortex filament flow. The spacecurves are spherical by with changing sphere radius.
Figure 9 depicts an isoperiodic flow through elastic torus knots in $\mathbb{R}^3$ of spectral genus 1, from a 2-wrapped circle to a 3-wrapped circle. In contrast to isospectral flows, the spectral curve changes during isoperiodic flow. Both flows preserve the closing of the spacecurves.
References
-
Leonhard Euler.
Methodus inveniendi lineas curvas maximi minimive proprietate gaudentes, sive solutio problematis isoperimetrici lattissimo sensu accepti.
1744.
URL: eulerarchive.org. -
Christoph Bohle, Paul Peters, and Ulrich Pinkall.
Constrained Willmore surfaces.
Calc. Var. Partial Differential Equations, 2008.
URL: https://mathscinet.ams.org/mathscinet-getitem?mr=2389993. -
Lynn Heller.
Constrained Willmore tori and elastic curves in 2-dimensional space forms.
Comm. Anal. Geom., 2014.
URL: https://mathscinet.ams.org/mathscinet-getitem?mr=3210758. -
Martin Kilian, Martin Schmidt, and Nicholas Schmitt.
Flows of constant mean curvature tori in the 3-sphere: The equivariant case.
preprint, 2010.
arXiv:1011.2875.