Supercyclidic Nets

Description

---

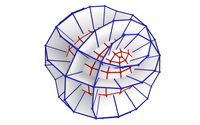
Supercyclides are surfaces with a characteristic conjugate parametrization consisting of two families of conics. Patches of supercyclides can be adapted to a Q-net (a discrete quadrilateral net with planar faces) such that neighboring surface patches share tangent planes along common boundary curves. The resulting patchworks are called "supercyclidic nets", and every Q-net in $\mathbb{R}P^3$ can be extended to a supercyclidic net. The construction is governed by a multidimensionally consistent 3D system. One essential aspect of the theory is the extension of a given Q-net in $\mathbb{R}P^N$ to a system of circumscribed discrete torsal line systems. The latter can be described in terms of projective reflections generalizing the systems of orthogonal reflections which govern the extension of circular nets to cyclidic nets by means of Dupin cyclide patches.

References

---

Authors

See also