Discrete Conformal Maps

Alexander I. Bobenko, Stefan Sechelmann, Boris Springborn

Description

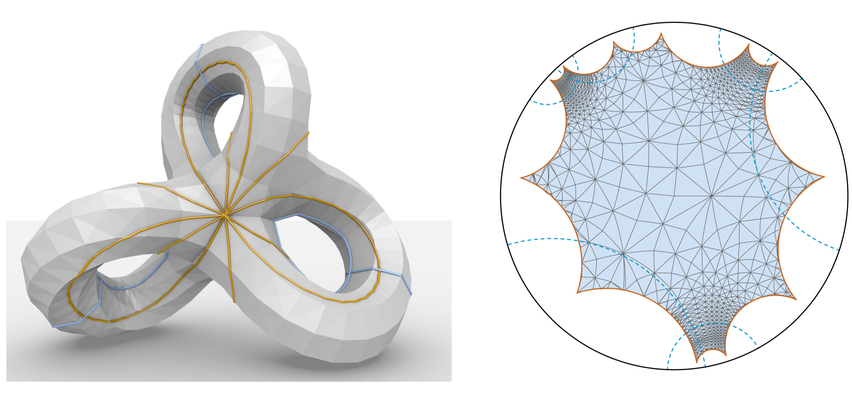
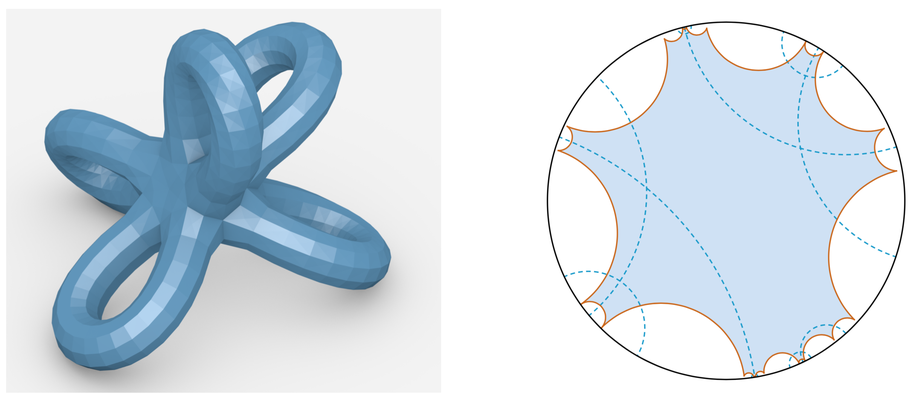
The notion of discrete conformal equivalence for polyhedral surfaces is based on a simple definition:
Two polyhedral surfaces are discretely conformally equivalent if the edge lengths are related by scale factors assigned to the vertices. It leads to a surprisingly rich theory.

The notion of discrete conformal equivalence is extended from triangulated surfaces to polyhedral surfaces with faces that are inscribed in circles.

References

  • A. I. Bobenko, S. Sechelmann, and B. Springborn.
    Discrete conformal maps: Boundary value problems, circle domains, Fuchsian and Schottky uniformization.
    In A. I. Bobenko, editor, Advances in Discrete Differential Geometry. Springer, 2016.
    dgd:194.

Authors

Prof. Dr. Alexander I. Bobenko   +

Projects: A01, A02, B02, C01, CaP, Z
University: TU Berlin, Institut für Mathematik, MA 881
Address: Straße des 17. Juni 136, 10623 Berlin, GERMANY
Tel: +49 30 31424655
E-Mail: bobenko[at]math.tu-berlin.de
Website: http://page.math.tu-berlin.de/~bobenko/

Dr. Stefan Sechelmann   +

University: TU Berlin
E-Mail: sechel[at]math.tu-berlin.de

Prof. Dr. Boris Springborn   +

Projects: A01
University: TU Berlin, Institut für Mathematik, MA 871
Address: Straße des 17. Juni 136, 10623 Berlin, GERMANY
Tel: +49 30 31423617
Fax: +49 30 31479282
E-Mail: boris.springborn[at]tu-berlin.de
Website: http://page.math.tu-berlin.de/~springb/

See also

Discrete Uniformization of Finite Branched Covers over the Riemann Sphere via Hyper-ideal Circle Patterns
Alexander I. Bobenko, Nikolay Dimitrov, Stefan Sechelmann
images
Lawson's Surface Uniformization
Alexander I. Bobenko, Stefan Sechelmann, Boris Springborn
images other
Antiparallelograms
Tim Hoffmann, Jürgen Richter-Gebert
Cinderella models images
A Reflectionless Discrete Perfectly Matched Layer
Albert Chern
videos images