Canonical Möbius Subdivision

Description

---

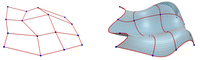
A novel framework for creating Möbius-invariant subdivision operators with a simple conversion of existing linear subdivision operators is presented. With this, a wide variety of subdivision surfaces that have properties derived from Möbius geometry; namely, reproducing spheres, circular arcs, and Möbius regularity, are obtained. The respective method is based on establishing a canonical form for each 1-ring in the mesh, representing the class of all 1-rings that are Möbius equivalent to that 1-ring. This is done by performing a chosen linear subdivision operation on these canonical forms, and blending the positions contributed from adjacent 1-rings, using two novel Möbius-invariant operators, into new face and edge points. The generality of the method allows for easy coarse-to-fine mesh editing with diverse polygonal patterns, and with exact reproduction of circular and spherical features. The operators are in closed-form and their computation is as local as the computation of the linear operators they correspond to, allowing for efficient subdivision mesh editing and optimization.

References

---

Authors

See also