Regular Meshes from Polygonal Patterns
Christian Müller, Amir Vaxman, Ofir WeberMedia
Description
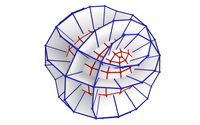
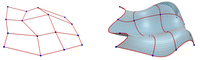
The goal is to design shapes from diverse combinatorial patterns, where the vertex 1-rings and the faces are as rotationally symmetric as possible, where such meshes are defined as regular. Designers and artists are allowed to envision and realize original meshes with great aesthetic qualities. The method is general and applicable to meshes of arbitrary topology and connectivity, from triangle meshes to general polygonal meshes. The designer controls the result by manipulating and constraining vertex positions. A novel characterization of regularity is offered, using quaternionic ratios of mesh edges, and optimize meshes to be as regular as possible according to this characterization. A mathematical analysis of these regular meshesshows how they relate to concepts like the discrete Willmore energy and connectivity shapes.
References
-
Amir Vaxman, Christian Müller, and Ofir Weber.
Regular meshes from polygonal patterns.
ACM Transactions on Graphics (TOG), 36(4):113, 2017.
doi:10.1145/3072959.3073593.