Smoothness of Polyhedral Surfaces
Felix Dellinger, Felix Günther, Caigui Jiang, Martin Kilian, Davide Pellis, Helmut Pottmann, Johannes WallnerDescription
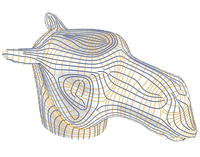
Polyhedral surfaces are fundamental objects in architectural geometry and industrial design. Whereas closeness of a given mesh to a smooth reference surface and its suitability for numerical simulations were already studied extensively, the aim is to find and to discuss suitable assessments of smoothness of polyhedral surfaces that only take the geometry of the polyhedral surface itself into account. Motivated by analogies to classical differential geometry, a theory of smoothness of polyhedral surfaces including suitable notions of normal vectors, tangent planes, asymptotic directions, and parabolic curves that are invariant under projective transformations is proposed. It is remarkable that seemingly mild conditions significantly limit the shapes of faces of a smooth polyhedral surface. Besides being of theoretical interest, the smoothness of polyhedral surfaces might be of interest in the architectural context, where vertices and edges of polyhedral surfaces are highly visible.
Furthermore, representing smooth geometric shapes by polyhedral meshes can be quite difficult in situations where the variation of edges and face normals is prominently visible. Especially problematic are saddle-shaped areas of the mesh, where typical vertices with six incident edges are ill suited to emulate the more symmetric smooth situation. The importance of a faithful discrete representation is apparent for certain special applications like freeform architecture, but is also relevant for simulation and geometric computing.
We discuss what exactly is meant by a good representation of saddle points, and how this requirement is stronger than a good approximation of a surface plus its normals. We characterize good saddles in terms of the normal pyramid in a vertex. We show several ways to design meshes whose normals enjoy small variation (implying good saddle points). For this purpose we define a discrete energy of polyhedral surfaces, which is related to a certain total absolute curvature of smooth surfaces. We discuss the minimizers of both functionals and in particular show that the discrete energy is minimal not for triangle meshes, but for principal quad meshes. We demonstrate our procedures for optimization and interactive design by means of meshes intended for architectural design.
References
-
D. Pellis, M. Kilian, F. Dellinger, J. Wallner, and H. Pottmann.
Visual Smoothness of polyhedral surfaces.
ACM Trans. Graphics, 2019.
URL: http://hdl.handle.net/10754/653104. -
Felix Günther, Caigui Jiang, and Helmut Pottmann.
Smooth polyhedral surfaces.
preprint, March 2017.
arXiv:1703.05318.