Discrete Uniformization of Finite Branched Covers over the Riemann Sphere via Hyper-ideal Circle Patterns
Alexander I. Bobenko, Nikolay Dimitrov, Stefan SechelmannDescription
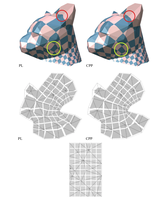
With the help of hyper-ideal circle pattern theory, a discrete version of the classical uniformization theorems for surfaces represented as finite branched covers over the Riemann sphere as well as compact polyhedral surfaces with non-positive curvature was developed.
References
-
A. I. Bobenko, N. Dimitrov, and S. Sechelmann.
Discrete uniformization of finite branched covers over the Riemann sphere via hyper-ideal circle patterns.
preprint, 2015.
arXiv:1510.04053.