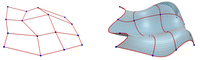
Discrete Confocal Quadrics
Alexander I. Bobenko, Wolfgang K. Schief, Yuri Suris, Jan TechterDescription
Presented are the integrable system and geometric approach on the discretization of confocal conics.
Confocal quadrics lie at the heart of the system of confocal coordinates (also called elliptic coordinates, after Jacobi).
In the integrable system approach a discretization which respects
(1) separability,
(2) all two-dimensional coordinate subnets being isothermic surfaces that is, allowing a conformal parametrization along curvature lines, or, equivalently, supporting orthogonal Koenigs nets, (both being crucial properties of confocal coordinates) is suggested.
The construction is based on an integrable discretization of the Euler-Poisson-Darboux equation and leads to discrete nets with the separability property, with all two-dimensional subnets being Koenigs nets, and with an additional novel discrete analog of the orthogonality property. The coordinate functions of the discrete nets are given explicitly in terms of gamma functions.
The geometric approach is based on a novel characterization thereof as factorizable orthogonal coordinate systems.
This leads to factorizable discrete nets with a novel discrete analog of the orthogonality property. A discrete confocal coordinate system may be constructed geometrically via polarity with respect to a sequence of classical confocal quadrics. Various sequences correspond to various discrete parametrizations. The coordinate functions of discrete confocal quadrics are computed explicitly. The theory is illustrated with a variety of examples in two and three dimensions. These include confocal coordinate systems parametrized in terms of Jacobi elliptic functions. Connections with incircular (IC) nets and a generalized Euler-Poisson-Darboux system are established.
References
-
Alexander I. Bobenko, Wolfgang K. Schief, Yuri B. Suris, and Jan Techter.
On a discretization of confocal quadrics. I. An integrable systems approach.
Journal of Integrable Systems, 1(1):xyw005, 2016.
arXiv:1511.01777, doi:10.1093/integr/xyw005. -
Alexander I Bobenko, Wolfgang K Schief, Yuri B Suris, and Jan Techter.
On a Discretization of Confocal Quadrics. A Geometric Approach to General Parametrizations.
International Mathematics Research Notices, December 2018.
arXiv:1708.06800, doi:10.1093/imrn/rny279.