Projects
Active Projects of the SFB Transregio 109
A01: Discrete Riemann Surfaces
- Investigating the Facets of Discrete Complex Analysis
- Alexander Bobenko, Ulrike Bücking, Boris Springborn
-
Riemann surfaces arise in complex analysis as the natural domain of holomorphic functions. They are oriented two-dimensional real manifolds with a conformal structure. Several discretizations of Riemann surfaces exist, e.g., involving discretized Cauchy-Riemann equations, patterns of circles, or discrete conformal equivalence of triangle meshes. Project A01 aims at developing a comprehensive theory including discrete versions of theorems such as uniformization, convergence issues and connections to mathematical physics.
A02: Discrete Parametrized Surfaces
- Developing a Theory of Discrete Surfaces with Constant Mean Curvature
- Alexander Bobenko, Tim Hoffmann
-
In recent years, an exhaustive theory has been developed to understand and construct discrete minimal surfaces. We aim to produce something similar for the construction and classification of discrete surfaces with constant mean curvature (cmc). In particular, for discrete minimal surfaces the study of Koebe polyhedra that serve as Gauß maps has been fruitful - we are interested in analoga for discrete surfaces with constant mean curvature.
A05: Conformal Deformations of Discrete Surfaces
- The Construction of a Discrete Differential Geometry Version of Certain Conformal Deformations
- Ulrich Pinkall, Olga Diamanti
-
Two geometries can be considered equivalent if there exists an angle preserving transformation between them; this is a so called conformal transformation. In the smooth case, conformal equivalences are quite well understood. However, mimicking their construction in the discrete case brought up not only interesting properties and algorithms, but also interesting problems - first and foremost the question of how to construct conformal deformations with certain prescribed properties.
A13: Geometry driven assembly of proteins
- Gero Friesecke, Myfanwy Evans
-
The assembly of proteins, and more generally their structure and shape in relation to function, have been a fascinating journey at the cutting edge of science over the past century. From Rosalind Franklin’s first X-ray scattering images of the DNA double helix and viruses to the modern protein structure databases, geometry has always played an important role in these fields of biochemistry. In this project we aim at a more rigorous understanding of the role of shape in one basic aspect of protein function, namely self-assembly, by combining recent ideas from biophysics, the concept of mixed volumes in differential geometry, and the mathematics of crystallization.
B02: Discrete Multidimensional Integrable Systems
- Classifying and Structuring Multidimensional Discrete Integrable Systems
- Alexander Bobenko, Yuri Suris
-
In recent years, there has been great interest among differential geometers for discovered discrete integrable systems, since many discrete systems with important applications turned out to be integrable. However, there is still no exhaustive classification of these systems, in particular concerning their geometric and combinatoric structure. Here, we investigate and classify multidimensional discrete integrable systems.
B08: Wigner crystallization
- Gero Friesecke
-
B09: Structure Preserving Discretization of Gradient Flows
- Analyzing Discrete Curves of Steepest Descent in Discrete Energy Landscapes
- Daniel Matthes, Oliver Junge
-
Many evolution equations from physics, like those for diffusion of dissolved substances or for phase separation in alloys, describe processes in which a system tries to reach the minimum of its energy (or the like) as quickly as possible. The descent towards the minimum is restrained by the system’s inertia. In this project, we discretize these evolution equations by optimizing discrete curves in a discrete energy landscape with respect to a discrete inertia tensor.
B10: Geometric desingularization of non-hyperbolic iterated maps
- A coherent theory for geometrically resolving singularities in time-discrete dynamical systems
- Christian Kühn, Yuri Suris
-
Singularities are ubiquitous in dynamical systems. They often mark boundaries between different dynamical regimes and also serve as organizing centers for the geometry of phase space and parameter space. In this project, we aim to extend geometric desingularization methods developed in the context of continuous-time systems to various classes of discrete-time maps as well as to desingularization of space-discretizations of fast-slow partial differential equations.
B11: Geometric rigidity in spin systems
- Marco Cicalese, Barbara Zwicknagl
-
The project B11 aims at developing a deeper understanding of typical low-energy states and to derive coarse-grained continuum theories of variational lattice spin theories. One of the main difficulties in this respect is the lack of understanding of elementary low-energy singularities such as vortices or line defects in spin systems. Our goal is to address these issues for simple but relevant lattice models. For that, we will combine methods from different areas: direct methods in the calculus of variations, abstract methods of Gamma-convergence and scaling laws analysis via domain branching constructions.
B12: Coarse cohomological models of dynamical systems
- Ulrich Bauer, Oliver Junge
-
Many processes (aka dynamical systems) in nature or technology exhibit complicated behavior. In particular, it is often inherently impossible to reliably predict future states of the process over long time spans. Reliable predictions, however, can be made on statistical or otherwise coarsened properties of the system. In this project, we construct coarse models of the behavior of a system which, in contrast to existing approaches, incorporate information about cycling motion, generalizing the classic notion of periodic or quasiperiodic dynamics.
C01: Discrete Geometric Structures Motivated by Applications and Architecture
- Geometry Supporting the Realization of Freeform Architecture
- Alexander Bobenko, Helmut Pottmann, Christian Müller
-
Contemporary architecture of large-scale buildings makes it necessary to subdivide large surfaces into smaller segments, the panels. While the building industry, architects and engineers are mainly interested in design aspects, manufacturing and statics, we will systematically investigate the related purely mathematical problems together with computational aspects. In particular we will investigate diagonal parametrizations, ring pattern structures, and discrete structures in sphere geometries.
C02: Digital Representations of Manifold Data
- Felix Krahmer
-
Whenever data is processed using computers, analog-to-digital (A/D) conversion, that is, representing the data using just 0s and 1s, is a crucial ingredient of the procedure. This project will mathematically study approaches to this problem for data with geometric structural constraints.
C04: Persistence and Stability of Geometric Complexes
- Ulrich Bauer, Herbert Edelsbrunner
-
The following more detailed questions are studied within this project: The definition and construction of geometric complexes from data. Topological persistence. The homology of dynamical systems. The convergence of variants of Crofton's formula obtained with persistent homology to compute intrinsic volumes. The approximation of persistent homology through simplification of the representative complexes.
C05: Computational and structural aspects in multi-scale shape interpolation
- Konrad Polthier, Daniel Cremers
-
Shape analysis is of central interest in computer vision and geometry processing. Three major computational and theoretical challenges in shape analysis are the computation of correspondences (shape registration or matching), the definition of similarity measures (metrics in shape space), and the generation of intermediate shapes (shape morphing).
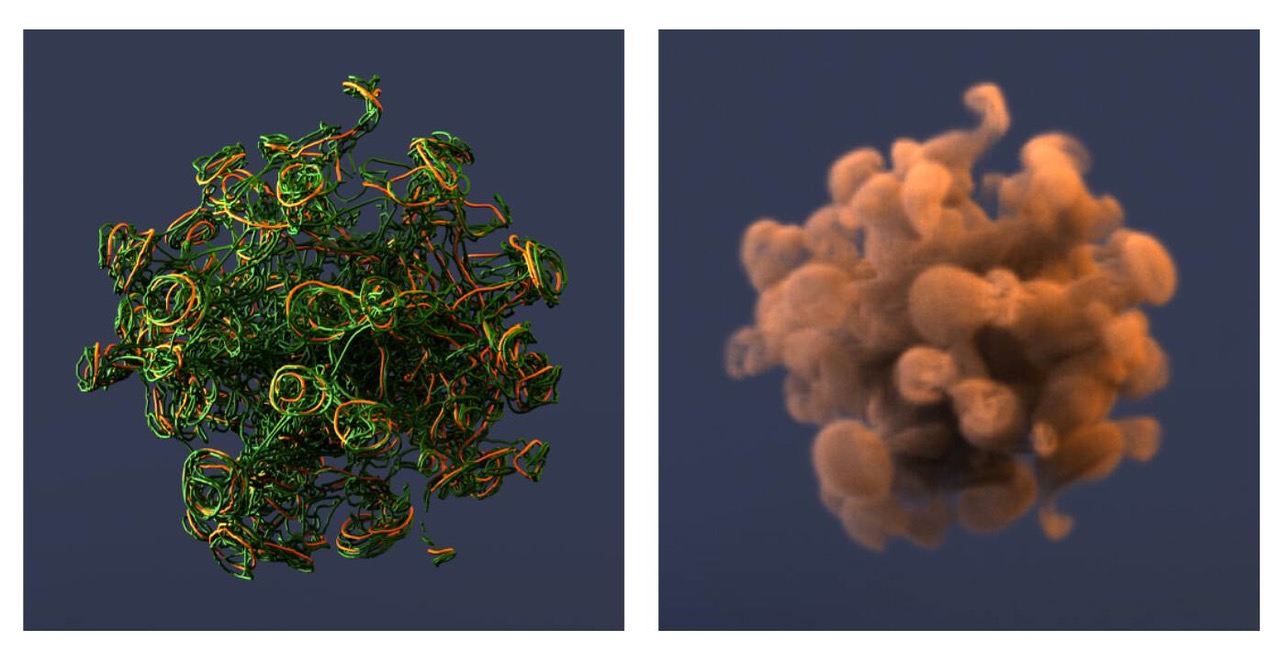
C07: Discretizing fluids into filaments and sheets
- Ulrich Pinkall, Nils Thuerey
-
In many situations important for physics simulation, the relevant fields (like the vorticity of a fluid or the magnetic field of a plasma) exhibit a strong tendency to become concentrated in one-dimensional filaments or two-dimensional sheets. “Decomposing” a given continuous field into its ”constituent” filaments or sheets is important for understanding and visualizing a given field. Moreover, simulation algorithms that take into account the natural tendency of the fields to become "discretized” into filaments or sheets can be highly efficient. We also will use the methods developed in this project to reconstruct velocity fields from video capture of smoke.
C09: Deep learning for shape reconstruction
- Gitta Kutyniok, Daniel Cremers
-
Shape reconstruction is one of the fundamental problems in computer vision. It can be formulated as an inverse problem given a collection of (2D) observations. Deep neural networks excel in these kind of settings, however, they do not work well with many common 3D shape discretizations, e.g. triangular meshes. In this project we will analyze which shape representations and neural network architectures benefit from one another, and develop new algorithms that allow fast, accurate reconstructions using deep learning.
CaP: Communication and Presentation
- Research on Transporting Maths Content from the SFB to the Public
- Alexander Bobenko, Günter Ziegler
-
Images from geometry can serve as a visual pathway into mathematics. In the SFB they are leading in particular into pioneer research. This is to be taken as an opportunity: We would like to learn more about how mathematics can be communicated by means of visual content. And we would like to communicate new results from the SFB.
Z: Central Tasks
- Alexander Bobenko
-